Alkulukuparit 2/3

ALKULUKUJEN ARVOITUKSET, OSA 5/9.

Tässä osassa tarkastelemme alkulukupareja analyyttisemmin. Edellisesti luvusta tiedämme jo, että alkuluvut pariutuvat, koska tekijät kohtaavat toisensa matriisin nollakohdassa ja koska matriisit ovat symmetrisiä. Pienimmät, tässä vaiheessa jo varsin hyvin tunnetut tekijät asettavat alkuluvuille tarkat rajat, joista ne eivät koskaan myöhemminkään voi poiketa.

Origo6 +1/-1

Tekijöiden 2 ja 3 tanssikuviosta seuraa, että kaikki alkulukuparit ovat ilmaistavissa kaavalla 6n + 1 sekä 6n -1. Itse asiassa myöskin kaikki ei-parilliset alkuluvut ovat jompaa kumpaa muotoa (ainoa poikkeus ovat tietenkin luvut 2 ja 3). Jokainen alkuluku on siis yhden askelen päässä kuudella jaollisesta luvusta.

Meidän ei kuitenkaan kannata tyytyä tähän. Voimme muotoilla alkuluvuille täsmällisemmät arvot tutkimalla matriisia, jossa on enemmän tunnettuja tekijöitä. Mikään ei aseta rajoja tällaiselle tutkimukselle: teoriassa voimme kertoa keskenään kuinka monta tekijää tahansa ja saamme uuden, suuremman matriisin.

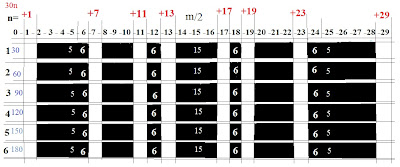
Origo30 - Alkulukuparit

Tässä kaavakuvassa luku 1 on merkitty alkuluvuksi (eli asetettu kultaiseen kehykseen) Syy on siin, ettei kyseessä ole todellinen luku 1 vaan luku "30n+1", toisin sanoen matriisin nollakohtaa seuraava luku. Esimerkiksi luvut 31, 61 tai 91 ovat tällaisia lukuja.

Koska luku 5 on tekijänä matriisissa, ei 30n + 5 tai 30n - 5 voi koskaan olla alkuluku. Tässä matriisissa pätee siis sama kuin meille tutummassa kymmenjärjestelmässä.

Luku viisi on vähentänyt alkulukuparien määrää kahdella. Origo30 antaa täsmällisempiä arvoja kuin Origo6, sillä siinä on useampia tunnettuja tekijöitä.

Kuvasta näemme, että alkuluvut ovat muotoa:

30n +1
30n -1

30n + 11
30n + 13

30n + 17
30n + 19

Jos haluamme, voimme hyödyntää symmetriaa ja ilmaista viimeisen parin myös muodossa:

30n - 11
30n -13

Nämä havainnot ovat täydellisesti yleistettävissä, kunhan suljetaan pois alkulukupari 5 sekä 7. Ehkä siis olisi parempi sanoa, että sääntö pätee kaikkiin alkulukupareihin, kunhan n > 0.

Kuviosta näemme myös, että kaikissa neljän tai kuuden alkuluvun ryppäissä on 15:lla jaollinen keskipiste.


Kirje professorille 2010

Tällaisia ilmiöitä olin siis havainnut jo vuoden 2010 alkupuoliskolla. Halusin tietää olenko oikeilla jäljillä - tai olenko mahdollisesti tehnyt jo tässä vaiheessa uusia havaintoja, joten lähetin sähköpostia muutamalle yliopiston tutkijalle ja dosentille, joiden tiesin erikoistuneen lukuteoriaan.

Eräs heistä vastasikin pian ja kertoi, että sähköpostissani esittämäni havainnot ovat tunnettuja ja todistettuja. Se oli tietenkin hyvä asia, sillä tiesin nyt olevani oikeilla jäljillä. Olin maininnut sähköpostissani vain murto-osan ajatuksistani ja olisi ehkä ollut järkevää jatkaa kirjeenvaihtoa heti silloin ja selvittää tarkemmin mitkä osat itsenäisistä tutkimuksistani jo tunnettiin lukuteoriassa. Omien todistusten muotoilu ja metodi, jolla niihin oli päästy kuitenkin vaikuttivat radikaalisti eroavan aiemmasta - ainakin saatavilla olevan kirjallisuuden ja nettisivustojen perusteella.

Käytännössä kaikki 1900-luvun edistysaskelet lukuteoriassa perustuivat logaritmiin ja alkulukulauseeseen:
http://fi.wikipedia.org/wiki/Alkulukulause
Tästä syystä ne ovat epätäsmällisiä, eivätkä palvele arkiymmärrystä. Todistukset on johdettu aiemmista todistuksista ja niiden selittäminen edellyttää monimutkaisten yhtälöiden opettelemista.

Entä mitä Wikipedia meille kertoo "tekijöistä"?
http://fi.wikipedia.org/wiki/Tekij%C3%A4

"Tämä matematiikkaan liittyvä artikkeli on tynkä."

Niinpä tietenkin. :D


Pimeä matriisi, The Dark Matrix

Kun tekijät tunnetaan, ne voidaan sulkeistaa pois ja unohtaa. Syntyy pimeä matriisi, jossa huomion voi helpommin kiinnittää alkulukuihin tai varteenotettaviin tekijöihin.

En ole piirtänyt tätä täydellisen mustaksi vaan jättänyt matriisin solmukohdat näkyviin, siis 6:lla jaolliset luvut sekä osan viitosen sijaineista.

Ruudokossa ovat siis vasemmalta oikealle ja ylhäältä alas merkittynä kaikki kokonaisluvut nollasta 210:een. (Tai jos täsmällisiä ollaan niin 7 - 209) Kaikki alkuluvut tuolta väliltä löydetään avonaisista ruuduista - ja niitä on paljon. Seuraavaan kuvaan olen merkinnyt alkuluvut punaisella ruksilla ja ei-alkuluvut mustalla.

KLIKKAA ISOMMAKSI!

Matriisin Origo210 aukkokohdat, eli kaikki alkuluvut välillä 0 - 210.

On lyhyempi luetella ne matriisin aukkokohdat, jotka eivät ole alkukuja: 12 /56  vs. 44 /56

49 = 7 x 7
77 = 7 x 11
91 = 7 x 13
119 = 7 x 17
121 = 11 x11
133 = 7 x 19
143 = 11 x 13
161 = 7 x 23
169 = 13 x 13
187 = 11 x 17
203 = 7 x 29
209 = 11 x 19

Origo30-ruudukkoa voi jatkaa niin pitkälle kuin halutaan ja aina alkuluvut löytyvät samoista sarakkaista. Turha siis väittää, että alkulukujen esiintymisessä olisi jotain outoa tai maagista. Nehän seisovat aivan maltillisesti suorissa riveissä kuin armeijan alokkaat paraatipäivänä.


Matriisi 30 x 7, eli Origo210

Jos luvun 7 liikkeet huomioidaan ja lasketaan mukaan seuraavan 210 numeron sarjaan, saadaan matriisi Origo210, johon myös voidaan laskea täsmälliset - aiempaa matriisia hieman tarkemmat - alkulukuparien ilmaantumiskohdat. Kaikkiaan ratkaisuja on 15 kpl, ja tilaa säästyy jos ne ilmaistaan symmetrisesti:

210n + 1  ja  210n -1

210n +/- 11 ja 13

210n +/- 17 ja 19

210n +/- 29 ja 31

210n +/- 41 ja 43

210n +/- 59 ja 61

210n +/- 71 ja 73

210n +/- 101 ja 103

Huomaa, että kohdassa 210n-1 ei ensimmäisellä näkemällä ole alkulukuparia! Kun n saa arvon 1, aukkokohdassa 210n - 1 = 209 seikkailee tekijä 11 (11 x 19). Myöhemmillä kierroksilla sijainti on kuitenkin jälleen vapaa ja alkulukuja putkahtaa esiin. Kyseessä on siis potentiaalinen sijainti alkulukuparille. Joka tapauksessa matriisi 210.ssa on alkulukuparia varten tuossa kohtaa tilaa - hedelmällistä maaperää - ja myöhemmin siitä tulee löytymään alkulukuja - myös pariutuneita sellaisia.

(Esimerkiksi jo seuraava 2 x 210 - 1 / + 1, eli 419 ja 421 ovat alkulukupari.)

Myöskään kohdassa 210n - 41 = 169  (13 x 13) ei ole alkulukuparin toista osapuolta, vaikkakin luotan, että samalla funktiolla 210n - 41 kyllä löytyy alkulukuja ja parejakin myöhemmin. Kaikkiaan tarkastelemassamme matriisissa toteutuu N:n arvolla 0 vain 13/15 mahdollisesta alkulukuparista. Muutaman puuttuminen selittyy varteenotettavilla tekijöillä 11 ja 13. Selitän myöhemmin miksi alkulukupareja toteuttavia funktioita 210n +/- X tulisi olla juuri 15 kpl, eikä vähempää

(Luvut 1427 ja 1429 ovat alkulukupari muotoa 210n -41 ja - 43. N saa arvon 7. Metodini ovat alkeelliset, mutta tässä vaiheessa teoreemani löytää jo alkulukuja jotka ovat käsitettävän avaruuden ulkopuolella - teoreemaan perustuvia, mutta toteutuvia.)

Luvun 210 jälkeen alkulukupareja löytyy vain ja ainoastaan yllä mainituilla koordinaateilla - äärettömyyteen asti. Jos haluamme jatkaa, voimme rakentaa seuraavan matriisin 210 x 11 = 2310 - ja sitä seuraavan 2310 x 13 - ja sitä seuraavan ja sitä seuraavan. Matriisissa Origo2310 tulisimme löytämään 135 alkulukuparia muotoa 2310n +X. Luku tulee aina olemaan pariton, koska jokainen matriisi on sisäisesti symmetrinen, minkä lisäksi on pariton alkulukupari muotoa + 1 / -1. Matriisin puolivälissä ei koskaan voi olla alkulukua tai alkulukuparia. Selitän seuraavassa osassa miten luku 135 on laskettu - ja kuinka voin olla varma siitä, että se pätee tarkasti.

Esittelemilläni metodeilla emme löydä ainoastaan tiettyjä suuria alkulukupareja vaan kaikki potentiaaliset alkulukuparien kohdat nollasta aina haluamaamme lukuun saakka... mutta vain potentiaaliset sijainnit. Jos haluamme eksakteja lukuja, tarvitsemme lisää välineitä.


Varteenotettavat tekijät

Luvusta 7 on tulossa seuraava tunnettu tekijä. Mitä me voimme tietää siitä, ilman että mekaanisesti käymme lävitse matriisin jokaisen ruudun?

Tässä vaiheessa on syytä huomata, että kulkiessaan matriisin nollakohdasta "0" uuteen nollakohtaan "210" numero 7 täyttää matkallaan aukkokohtia täsmälleen niin paljon kuin matriisissa alkujaan on: 8 kpl.

Huom. Katso ylempää lista luvuista jotka eivät ole alkulukuja! Löydät vain 7 tapausta, mutta lisäksi luku 7 pilkistää matriisin rakosesta myös kohdassa 0x30 + 7. Ensi esiintymisellään luku on alkuluku, mutta tämä lasketaan kahdeksanneksi tapaukseksi, koska myöhemmin kyseinen tekijä löytyy aina tuosta ruudusta, eikä se enää ole viaton alkuluku. Mikään luku 210n + 7 ei voi olla alkulukua, jos n on suurempi tai yhtä suuri kuin 1, koska sen tekijänä on luku 7. Esimerkiksi 217 ei ole alkuluku, eikä liiemmin 427. Ne sijaitsevat 7 askelen päässä nollakohdasta, jossa on tunnettuna tekijänä luku 7.
 
Seuraavassa luvussa todistan, että nämä havainnot on yleistettävissä miten suuriin matriiseihin tahansa.

Matkallaan kohti Origoa210 luku 7 kulkee seitsemän kertaa edellisen matriisin halki. (Tietenkin, koska 210:30 = 7.)  Se täyttää tarkalleen 1/7 kaikista mahdollisista aukkokohdista. Koska matriisissa Origo30 on 8 aukkoa, ja matriiseja on seitsemän kappaletta, jää jäljelle täsmälleen 6/7. Jos muissa kohdissa ei ole alkulukua tai luku 7 ei vieraile niissä, täytyy asialla olla tekijä 11, 13, 17, 19 jne.

Jatkuu...


PS. Ruudun 210n+7 tekijänä ei seitsemän lisäksi voi koskaan olla 2, 3 tai 5. Sama pätee kaikkiin matriisin Origo210 aukkokohtiin, joissa 7 on havaittu. Niinpä näissä on 7:n ohella jokin muu alkuluku tai kyseessä on seitsemän korkeampi potenssi.